INTRODUCCION:
En el presente trabajo estudiaremos el método de las líneas de influencia, para establecer condiciones cuando actuan una carga viva o variable de tal manera que produzca efectos máximos de corte, flexión, reacciones y deflexiones tanto para cargas puntuales como para cargas distribuidas.
La línea de influencia es un grafico que define la variación de un esfuerzo (corte, momento flector o torsor), reacción o deflexión en un punto fijo de la estructura a medida que se mueve una carga unitaria sobre ella.
Este método se utiliza mucho para cargas vivas sobre puentes, puentes grúas, bandas transportadoras y especialmente en aquellas estructuras con cargas móviles.
Cuando un camión, un vagón de ferrocarril u otros vehículos ruedan sobre una viga, constituyen un sistema de cargas concentradas, separadas por distancias fijas, que se llama tren de cargas. Como se ha visto, en vigas sobre las que solamente existen fuerzas concentradas, el máximo momento flexionante tiene lugar en el punto de aplicación de una fuerza, y en el caso de un tren de cargas móviles, el problema consiste en la determinación de los momentos en cada carga, cuando cada una de está en una posición tal que el máximo momento tenga lugar bajo ella. El mayor de tales momentos máximos es el que se ha de considerar en el diseño de la viga.
OBJETIVOS:
Conocer el comportamiento de una viga cuando está sometida a cargas móviles. Aprender a trazar bien las líneas de influencia en una viga isostática para que de esa manera poder realizar los cálculos respectivos. Conocer los conceptos básicos y fundamentales de las líneas de influencia para no tener dudas al momento de aplicarlo. Ampliar nuestros conocimientos frente a las deformaciones que ocurren en una estructura (vigas isostática ).
DEFINICION:
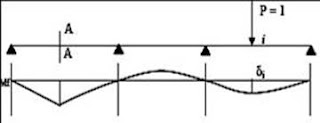
El concepto de línea de influencia, fue utilizada por primera vez por el profesor E. Winkler de Berlín, en 1876. Estas nos muestran gráficamente la forma en que el movimiento de una carga unitaria a lo largo de una estructura, influye en cierto efecto mecánico en la misma. Entre los efectos que pueden considerarse están las reacciones, fuerzas cortantes, momentos flexionantes, fuerzas axiales, deflexiones, etc. La línea de influencia puede definirse como una grafica cuyas ordenadas representan la magnitud y el carácter o sentido de cierta función o efecto en una estructura, a medida que una carga unitaria móvil se desplaza alo largo de la misma. Cada ordenada del diagrama define el valor de la función cuando la carga móvil se encuentra colocada en el sitio correspondiente a dicha ordenada. En la viga mostrada definiremos la sección A-A, en la cual diremos que Mf(A) es la Línea de Influencia del momento flector en A, si se cumple que la ordenada δi representa el valor del momento flector en A para una carga P=1 aplicada en el punto i.
Las líneas de influencia se utilizan primordialmente para calcular ciertas fuerzas y determinar posiciones de cargas vivas que produzcan fuerzas críticas o máximas. El procedimiento para dibujar los diagramas de la línea de influencia consiste simplemente en la graficación de los valores de la función en estudio, como ordenadas correspondientes a diversas posiciones de la carga unitaria a lo largo del claro y finalmente en unir por líneas los extremos de dichas coordenadas.
El procedimiento para dibujar los diagramas de la línea de influencia consiste simplemente en la graficación de los valores de la función en estudio, como ordenadas correspondientes diversas posiciones de la carga unitaria a lo largo del claro, y, finalmente, en unir por líneas los extremos de dichas coordenadas.
Por lo tanto se debe seguir mentalmente a la carga en su movimiento a lo largo del claro, tratando de imaginar que sucede cuando se desplaza al efecto que se considera. El análisis por líneas de influencia puede aumentar inmejorablemente el conocimiento de lo que sucede a una estructura en diferentes condiciones de carga. Considerando la forma en que actúan las cargas en una estructura vemos que se pueden clasificar en cargas permanentes (muertas), cargas no permanentes o vivas y/o cargas de construcción. La carga permanente, como su nombre lo dice, siempre estará presente en la vida útil de la estructura y producirá sobre esta efectos constantes; la carga viva o no permanente fluctúa tanto en posición sobre la estructura como en su duración produciendo efectos variables en ella. Podríamos concluir, de una manera apresurada, que colocando la carga viva sobre toda la estructura produciríamos los efectos máximos en ella, esta afirmación no es cierta y requiere de un estudio mas complejo.
Un ejemplo simple de este efecto es el de una viga simplemente apoyada con voladizo a un lado. Si la carga viva actúa sobre toda la viga, producirá un momento positivo en la luz menor que si actúa solo en el tramo apoyado; en este ejemplo sencillo nos percatamos de la importancia de saber colocar la carga para que produzca los efectos máximos y así cuando diseñemos no corramos el peligro de que nuestra estructura falle.

En este capítulo estudiaremos el método de las líneas de influencia para colocar la carga viva o variable de tal manera que produzca efectos máximos de corte, flexión, reacciones y deflexiones tanto para cargas puntuales como para cargas distribuidas.
La línea de influencia es un grafico que define la variación de un esfuerzo (corte, momento flector o torsor), reacción o deflexión en un punto fijo de la estructura a medida que se mueve una carga unitaria sobre ella.
La línea de influencia es diferente al diagrama de momento o cortante o a la elástica de la viga, estos representan la variación de la función a lo largo de la viga para una serie de cargas definidas y el otro define como varía V, M o δ en un punto específico cuando se mueve una carga unitaria sobre la viga no dando el valor de la función en toda posición.
La línea de influencia utiliza una carga unitaria ya que por los conceptos de linealidad, proporcionalidad y superposición se puede determinar la función especifica simplemente multiplicando el valor de la línea de influencia por el valor de la carga real.
Este método se utiliza mucho para cargas vivas sobre puentes, puentes grúas, bandas transportadoras y especialmente en aquellas estructuras con cargas móviles.
Determinación de la línea de influencia:
La línea de influencia es una gráfica en la cual las ordenadas representan una fuerza interna o deflexión y la abscisa representa la posición de una carga unitaria. Para su construcción se define el punto de estudio sobre la estructura, se comienza a variar la posición de la carga puntual y se encuentra el valor del esfuerzo interno a medida que se mueve la carga, se puede construir una tabla del valor de la función vs la posición de la carga y después se grafica. Otro método es encontrando la ecuación de la línea de influencia y graficando.
Construyamos la línea de influencia para la reacción en A de la siguiente viga:
Se empieza a mover la carga P a diferentes distancias x y para cada distancia se calcula RA.
Otro método es encontrando la ecuación de la variación de la reacción en A a medida que se mueve una carga unitaria. Se parte de encontrar esa reacción en función de la posición x de la carga P=1,0. Aplicando ecuaciones de equilibrio o encontrando la reacción por proporciones tenemos:

Notemos que la ecuación tiene pendiente negativa y con una variación lineal para RA.

Para obtener el valor de la reacción en A para cualquier carga P, se multiplica la ordenada de la línea de influencia por el valor de la carga.
Si L=8m, P=5 ton localizada a 3m del punto A el valor de la reacción sería:

Línea de influencia para el cortante en A: Se determina la variación del cortante en A por el método de las secciones:
En vista de que siempre es una carga puntual, se parte de encontrar primero las reacciones en función de la posición x y después se aplica el método de las secciones partiendo por el punto al cual se le quiere determinar la línea de influencia:

Haciendo equilibrio en la sección y localizando la carga en x>0 tenemos:

En este caso concluimos que la línea de influencia del cortante en A es igual a la de la reacción en A
Note que la línea de influencia se hacer para la convención positiva de los esfuerzos internos.
Línea de influencia para la reacción en B:


Línea de influencia para el momento en A:
Para cualquier posición de la carga unitaria el momento en A será cero.

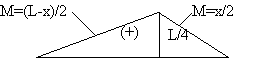
Línea de influencia para el cortante y momento en un punto C en L/2
Siempre comenzamos encontrando las reacciones en los apoyos y luego partimos:

Para x

, de donde


Para x>L/2 se toma la sección A-C para equilibrio:





Línea de influencia para el cortante en C:

Momento en C:
USO DE LAS LÍNEAS DE INFLUENCIA:
1. Caso de cargas puntuales: Para cualquier carga puntual P se multiplica el valor de la ordenada en el punto x y ese es el valor del corte o del momento o la función graficada.
Para encontrar los valores máximos de V o M se debe colocar la carga puntual P en el punto de máxima ordenada.
Ejemplo
Construya la línea de influencia para el cortante y momento en el punto B y diga en que puntos debe colocar una carga puntual para producir los máximos efectos de cortante y momento en B.

Encontremos las reacciones en función de x:




Líneas de influencia para corte y momento en B:
0 < x < 4m





Para 4
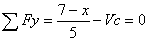



Líneas de influencia:
VB

MB

Se producen dos puntos donde puede actuar P y obtener el máximo momento en B, estos dos puntos son: x=0 y x=4m. Para el cortante se debe colocar la carga en x=4m para obtener el mayor cortante en B.
2. Caso de cargas distribuidas:
En realidad una línea de influencia para una carga distribuida no se podría encontrar como tal, pero la línea de influencia de la carga puntual se puede usar para determinar en que tramos colocar la carga distribuida para que produzca los valores máximos en un punto.
Si sabemos que el valor de la reacción, cortante o momento en un punto esta dado por la por la ordenada “y” de la línea de influencia multiplicada por el valor de la carga actuante P; entonces para una serie de cargas P, o sea una carga distribuida, el valor del cortante, momento o reacción se podría determinar por la suma de todos los cortantes o momentos de cada una de las cargas:
Para cargas distribuidas podemos considerar que cada carga P corresponde al valor de la carga distribuida por una longitud pequeña de viga Δx, dándonos la sumatoria como:
Notemos que el valor de la función conserva el signo de la grafica de la línea de influencia, así, si queremos obtener valores máximos debemos colocar la carga distribuida sobre áreas que sumen, con el signo correspondiente, a un valor existente.

Ejemplo
Determine donde debe colocar una carga distribuida para producir el mayor cortante negativo y momento en el punto ..C.

Para producir el máximo cortante negativo debemos cargar la viga en la zona de la línea de influencia con área negativa y para el momento máximo cargamos toda la viga ya que toda el área es positiva.


Ejercicio
Encontrar el máximo momento y el cortante máximo que se puede desarrollar en el punto C de la viga mostrada cuando está sometida a una carga permanente de 5000N/m. una carga viva distribuida de 1800 N/m y una carga puntual de 5000N.



Momento mínimo


Como hacer las líneas de influencia de una forma rápida?
Principio de Muller-Breslau
La de la línea de influencia en un punto dado para la cortante o momento esta dada por la deformada de la viga al aplicar ese momento o cortante en el punto determinado, retirando la capacidad de la viga para aguantar esa función.
Línea de influencia para reacción en A


Rodillo interno
Articulación

Las ordenadas de la línea de influencia de un esfuerzo cualquiera de una estructura son proporcionales a las de la curva de deformación que se obtiene al suprimir la restricción correspondiente a ese esfuerzo y aplicando en ese lugar el esfuerzo especificado.
Ejercicios:
Determine la forma de la línea de influencia para:





Lineas de influencia en armaduras y vigas en celosía
Para armaduras:
Se usa para determinar fuerzas axiales máximas en un miembro determinado.
La forma sería expresando la fuerza en un miembro determinado en función de la carga unitaria en cada uno de los nudos, otra es en función de la posición de x de la carga unitaria.
Pasos:
1. Expresar reacciones en función de la posición de carga unitaria.
2. Dividir la armadura en regiones antes y después del panel que contiene la barra a analizar.
3. Expresar la fuerza del miembro en función de las reacciones por el método de las secciones en las regiones no pertenecientes al panel.
4. Conectar las líneas de influencia en la región de la barra.